問題
南に1km進みます。
東に1km進みます。
北に1km進むとスタート地点と同じ場所に到着しました。
ここは地球上のどこでしょうか?
答え
実は答えは一つではありません。いくつもあります。
1つ目:一番わかりやすいのが、北極点です。
図で説明しますが、距離を正確に描くとよくわからなくなるので、縮尺は無視してください。
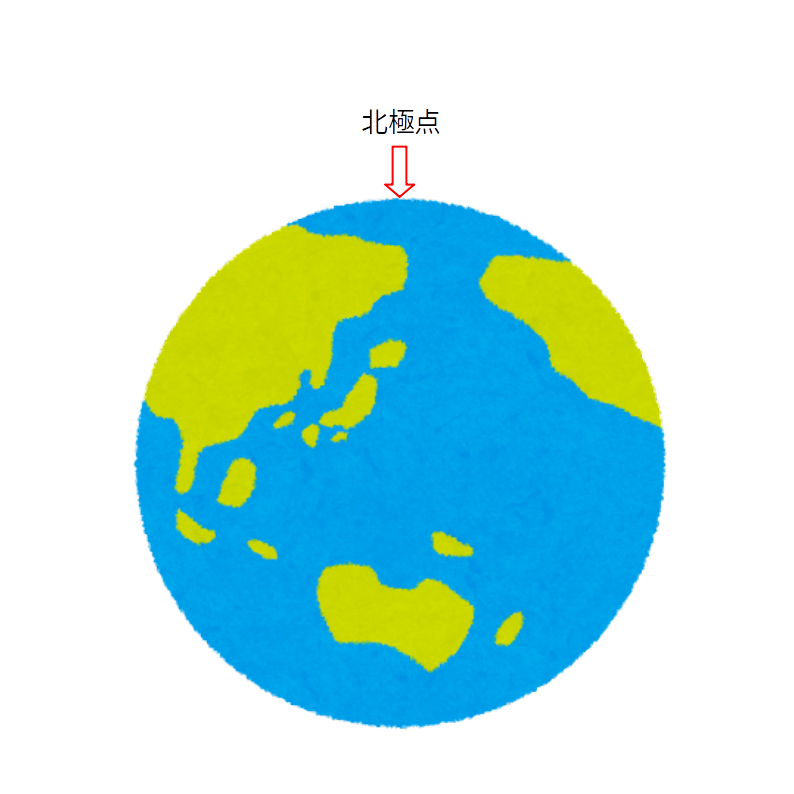
1.スタート地点の北極点から南へ1km進みます。
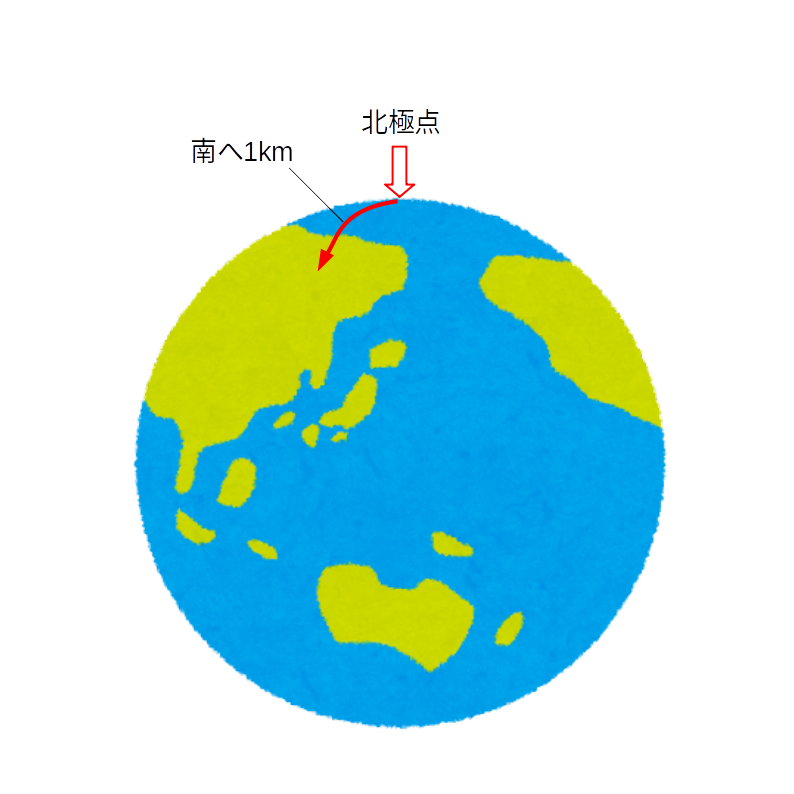
2.南へ1kmに到着したところから、東へ1km進みます。
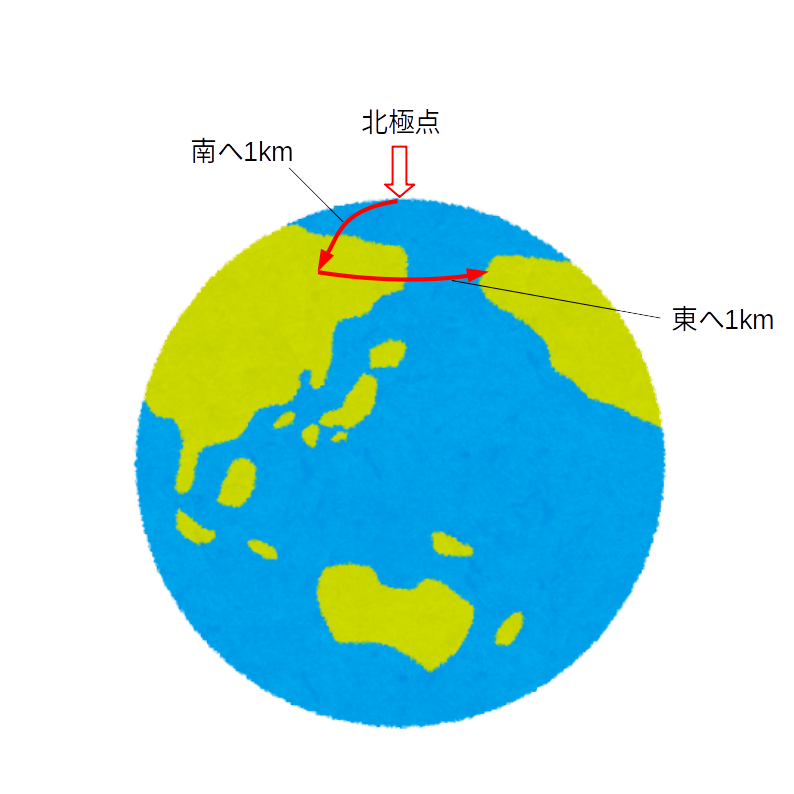
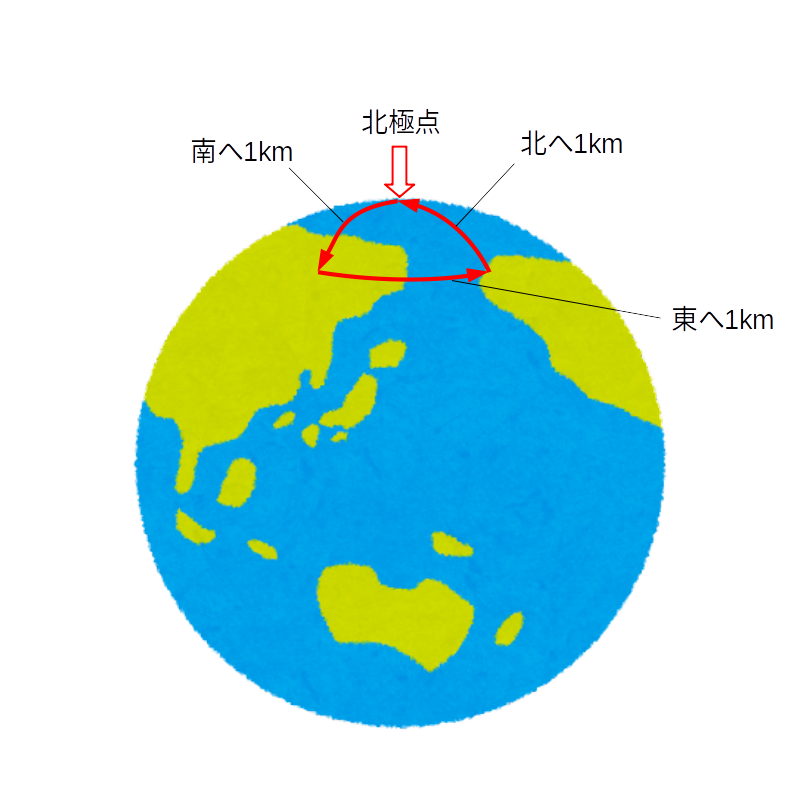
3.東へ1kmに到着したところから北へ1km進みます。
あら不思議?到着したところは、スタート地点の北極点に戻りました。
これで、回答できたと満足してしまいそうですが・・・
答えは他にあります。下の続きへ。
2つ目?の答え
実は無限にあります。
東へ1km進んだときに地球を1周して1kmになる緯度より、北に1km進んだ緯度上(円周上)のすべての地点になります。
ほぼ、南極点の付近となります。
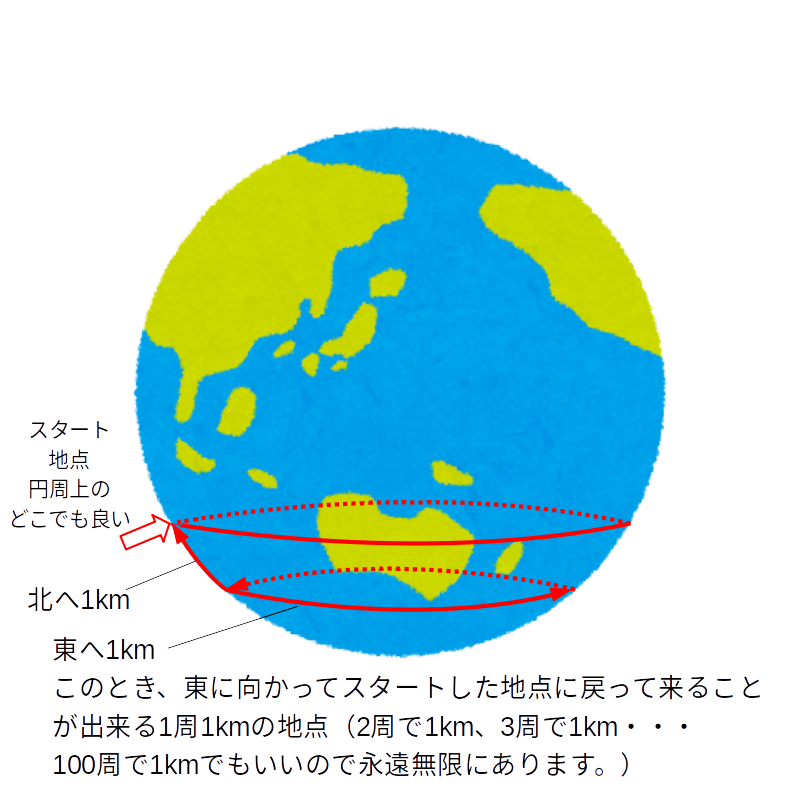
これは1km1周だけでなく、1kmで2周でも、3周でも100周でも1万周でも、東に向かい始めたスタート地点に1kmで戻ってこれれば良いわけです。それより北へ1kmの円周上で良いため、無限に地点があるということになります。その円周上ならね。
イメージは下の様な感じになります。

では、説明していきます。
スタート地点は円周上のどこでもいいですが、分かりやすいように1点で説明します。
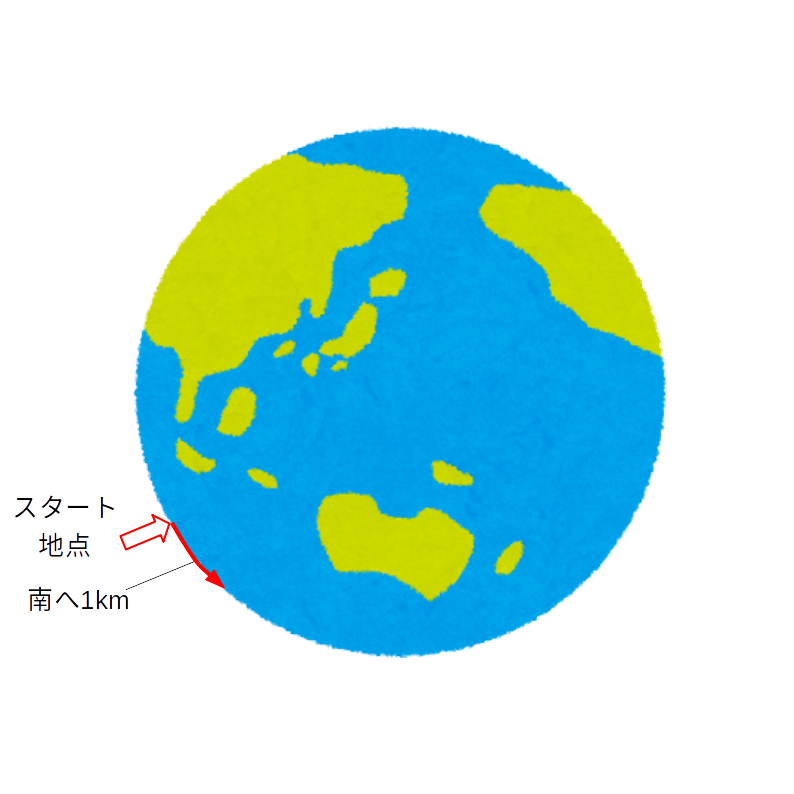
東へ1km進みます。
このとき、スタート地点に戻ってくれるように1周1kmの緯度でないといけません。
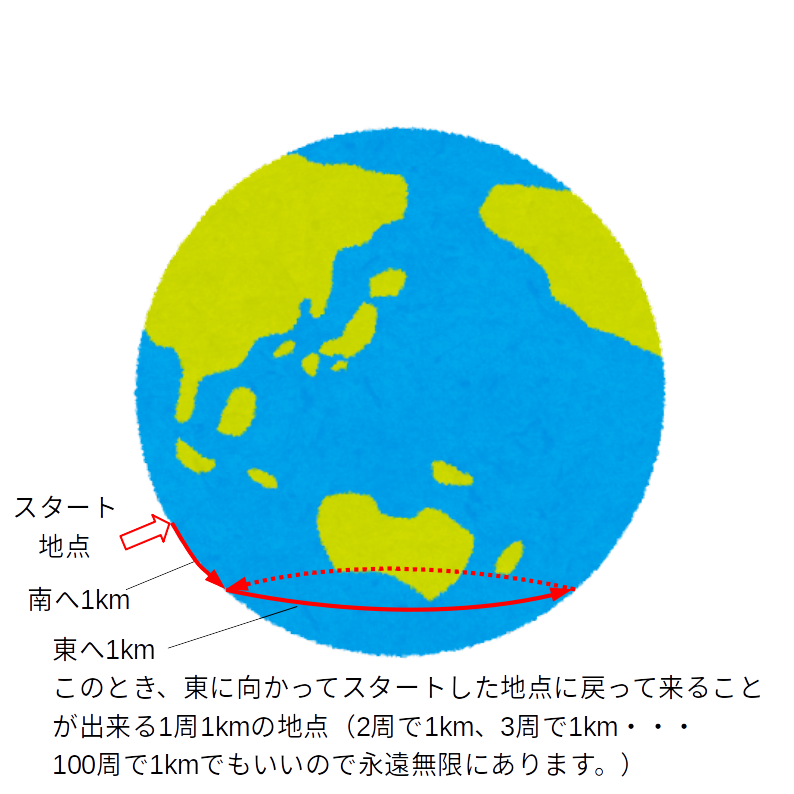
東に向かい始めたスタート地点にもどりますよね?
そこから北に1km進みます。
あら、不思議、到着したところはスタート地点にもどりました。
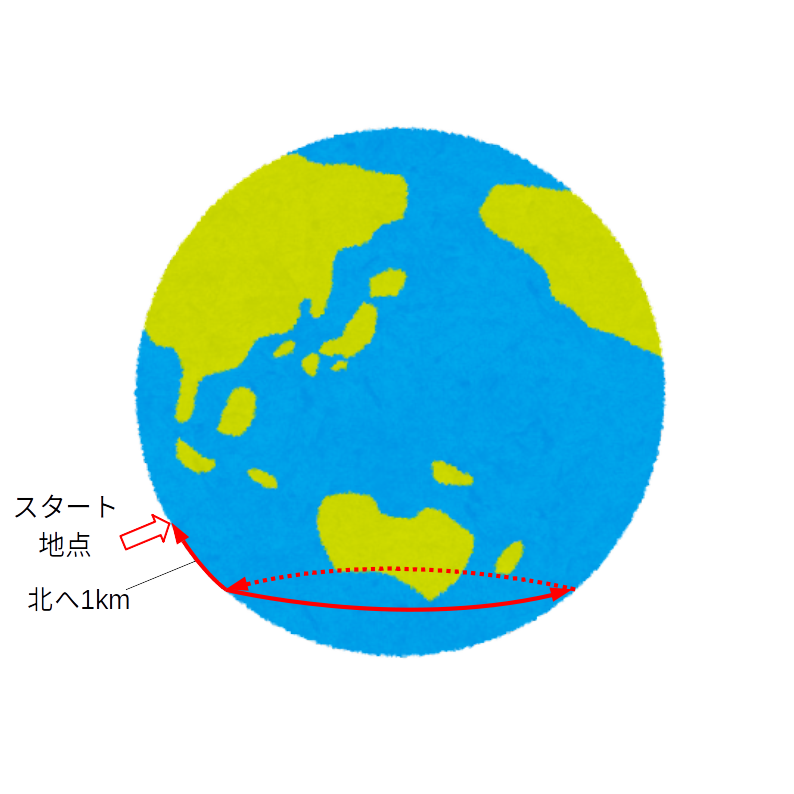
ということで、答えをまとめると。
答えは
- 北極点
- 1周1kmの緯度よりも北に1km行った緯度上。
- 1周0.5kmの緯度よりも北に1km行った緯度上。(2周回れば、東に向かうスタート地点に戻ります)
- 1周1/3kmの緯度よりも・・・
- 1周0.25kmの緯度よりも・・・
というように無限に元に戻る地点があります。
説明が下手なところがあると思いますので、わからなければ、コメントをいただければと思います。
#頭を使う問題
